很想写一些东西来总结总结自己的工作,可惜工作太忙一直也没顾得上来写。最近闲来想和大家讨论讨论关于创建用户模型的事情。
Persona:(Persona是用户模型的的简称)是虚构出的一个用户用来代表一个用户群。一个persona可以比任何一个真实的个体都更有代表性。
首先,用户模型是对用户的一种划分,是将一个类的概念转化成为一个角色。这里举一个简单的例子:电影里有很多角色,但是生活中有和电影中一模一样的角色么?显然是很少的,除非遇到极品。电影中人物的角色是集合了广大角色的共性而产生的角色代表,代表的是一类人或是一个群体。
用户是大量混杂的,我们需要将用户按照角色分开来确定不同角色的偏好与场景的结合,这才是建立persona体系的主要目的。
下面具体讲讲建立Persona体系的步骤。
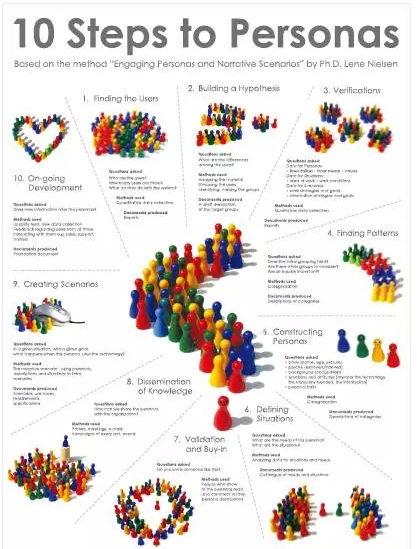
谈起建立Persona体系高手颇多,我这个菜鸟可不敢班门弄斧,我个人比较推崇Dr.Lene Nielsen的10步建立Persona方法。
-
Finding the users 发现用户
-
Building a hypothesis建立假设
-
Verifications调研
-
Finding patterns发现共同模式
-
Constructing personas构造虚构角色
-
Defining situations定义场景目标
-
Validation and buy-in复核与买进
-
Dissemination of knowledge知识的散布
-
Creating scenarios创建剧情
-
On-going development持续的发展
按照Dr.Lene Nielsen的方法可以建立起一套完整的用户模型体系(虽然有几条我也不是太会用),不过对于大多数产品这个方法还是有点高深莫测。
我刚接触这个玩意的时候看了一下午还是不太明白这玩意怎么用。所以只能基于这个高深玩意,自己总结了一套能够切实可行的Persona模型构造方法准备在下面简单说说,我本属菜鸟,大家多多提意见哦!
首先,要明确用户群体,这个在大多数应用开发之前就应该明确了。连用户群都不知道还开发个毛产品。其次,做出用户角色假设。这个时候大家就要问了,我本来就是要确定用户角色模型,这不是本末倒置了么??我要说明一点,在用户角色分析之前,我们要有个对用户划分的方向。比如对于一个游戏,我们要划分用户模型,其实有很多种分的方法。用户可以分为,初级玩家、中级玩家;还可以分为,战略性玩具、视觉性玩家、装备性玩家。
任何一个用户群体都有多种分类方式,首先要确定我们到底怎么来分类用户。确定了分类方式之后,再来一个一个分类来研究。
下面以一个我从事的互联网医疗产品作为一个简单的例子,来对这一点进行说明。这里只是简单举例,真正的用户模型假设分类远比例子复杂的多。
首先简单定义用户群:身体出现非紧急病症的人群。
如果是急症或是严重的病症一般会直接前往医院,并不会打开手机应用来咨询医生或者询问用药指导。所以我们的适用人群是身体出现异样且非紧急的人群。
做出假设,为了举例方便,我们简单的把用户角色分为:细心护理型、粗放型。细心护理型:主要是指非常注意自己的健康状况,不放过一点一滴的问题。粗放型:只需要知道个大概有事没事,不太关心自己的健康状态。我们先简单将用户角色分为这两种,继续第二步发分析。
对于这一步,可以通过少量用户访谈来完成,其实就是找到所有用户关注的点,我们将这些用户关注的点称为变量。
比如对于医疗产品,经过对用户的访谈,我们简略总结用户关注度为:医生的真实可靠性、医生的负责程度、能否找本地医生挂号、产品视觉、产品交互。为了举例方便,我们简单总结用户关注的这5个特点。从而可知,我们得到5个变量,下面将设计问卷分析出对不同角色用户对这5个变量的差异性。
问卷是针对我们产品真实用户群的调查,所以题目的设计必须非常具有针对性,并且通过结果能够达到我们预期的效果。
首先,要先将问卷问题分成三个区:甄别性问题区、变量问题区、建议性问题区。估计有人要问这都是些神马???其实这些很简单。甄别性问题,是用来甄别出用户属于哪个角色;比如我设置了10个问题,符合1,3,5条问题的用户属于角色A,符合2,4,6条问题的用户属于角色B。
甄别性问题:
以刚才的例子,我们简单设置3个甄别性问题:
Z1.您一般在线咨询病情的时间是多久?
A.<5min B.5-10min C.10-20min D.>20min
Z2.您是否需要随时的咨询医生?
A.需要 B.不需要 C.看情况
Z3.如果手上被划了一个小口子,并不是非常严重,您会?
A.立刻消毒包扎 B.清洗干净后该干嘛干嘛 C.压根不管
我们定义甄别规则如下:
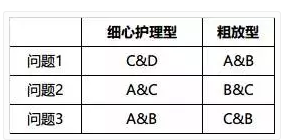
为了举例方便,我们简单给甄别角色设置了上述规则。这里说明几点,第一,规则是人设定的,可以更改,只有更好的规则,规则没有对错;第二,问题1、问题2、问题3之间是“与”的关系,问题内选项是“或”的关系。
有个问题,如果用户的答案都不满足于上面的规则,那如何分配用户角色呢???答案很简单:要么真正研究规则并修改规则;要么作为数据清洗将用户清洗掉(说明该用户没有认真答题,或是用户属于极小类群)。当然这个地方还有很多可以优化,具体参考数据挖掘资料。
变量性问题:
变量性问题其实是指针对用户关注的点进行问题设置。我们刚才举例总结出的关注点为:医生的真实可靠性、医生的负责程度、能否找本地医生挂号、产品视觉、产品交互,5个方面,针对每个方面可以设置1-n问题。(为了简便,每个变量仅列出一个问题)
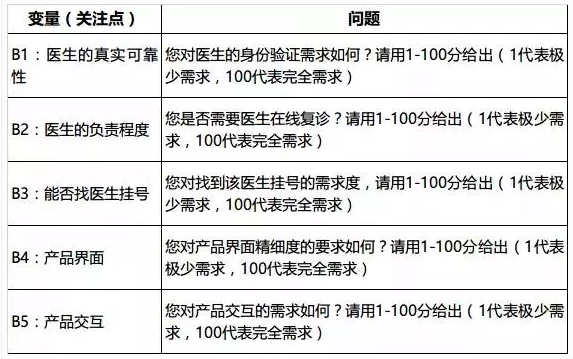
下面在列举出一个变量举出多个问题的例子:
产品交互:
-
您对页面扭转时的流畅性要求如何?请用1-100分给出(1代表不在意,100代表非常在意)
-
您对手机应用的操作频率如何?请用1-100分给出(1代表不经常,100代表经常操作)
-
您喜爱扁平化的交互设计还是深度立体的交互设计?请用1-100分给出(1代表喜欢扁平化的交互设计,100代表喜欢深度立体的交互设计)
…
总之,在设计变量性问题的时候,最好得到可量化的数字,这样方便于对以后的多元回归统计工作。
建议性问题:
建议性问题是不用用户角色给我们提出的要求,他们可能提出一些非全局的变量问题。比如,对于老年用户,可能会提出应用设计中存在放大镜功能,但这个功能明显不适合年轻人。建议性问题的很多可以设置成开放性问题,不用角色的用户可以将自己的想法写出来,如果大家都需要,那就变成了新需求,也就是产品功能的发展方向。
按照我们刚才的例子,给出2个建议性问题:
J1. 您作为用户还希望我们的应用添加什么样的功能?
-
语音服务功能
-
24小时服务电话
-
中英文
-
其他_______
J2. 您希望我们用什么方式和您联系?
-
电话
-
email
-
写信(哈哈,这里来个复古的方式)
-
直接上门
-
其他_______
到这里,我们的一套问卷就搭建完成了。
最后再说一句,在问卷的最后,要给出一个综合评价性的问题哦!!!!
综合满意度:
您对我们的应用满意度是什么?请用1-100分给出(1代表很不满意求,100代表非常满意)好啦,大功告成,这就是一套完整persona问卷。

上图描述了这一过程,其中每个颜色的小人,代表通过甄别问题后,区分出的用户角色。
最后用上面的问卷对10个用户进行访问,得到数据如下:
说明:
-
P1、P2、P3…P10代表10个用户;
-
Z1、Z2、Z3代表3个甄别性问题;
-
B1、B2、B3…B5代表5个变量性问题;
-
J1、J2代表2个建议性问题
-
甄别性问题结果:

按甄别问题对用户分类如下:
-
细心护理型:P1、P2、P4、P5、P10
-
粗放型:P6、P7、P9
-
数据异常问卷:P3、P8
异常数据的产生通常是由2个原因造成的,第一个是甄别逻辑设置不完善,比如我们这个例子甄别性问题少,很多情况都没有考虑清楚,所以在设计甄别问题时,尽量将所有情况思考清楚,以免出现过多无效数据;第二个是被调查用户填写不认真,这也是个很常见的问题,在设置问题时,尽量减少繁琐问题,使被调查用户能够比较准确的完成所有问题。
变量性问题结果:
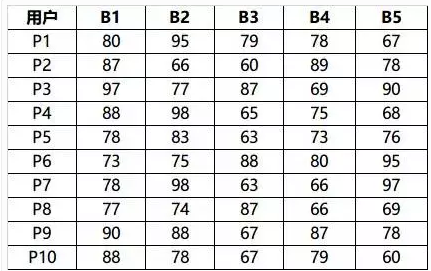
用户的调查结果以数表的形式展示出来,这样有利于进行多元回归分析。
建议性问题结果:
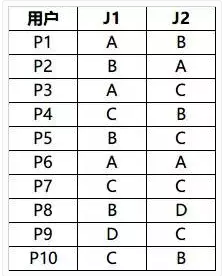
综合满意度:
![]()
数据的常规处理
对于刚才得到的数据,可以进行常规的处理。即求出平均值或者份额进行相应比较分析,所得到的结果如下。
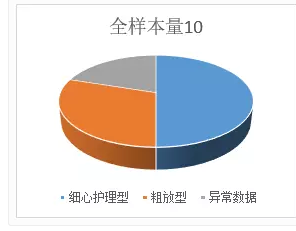
对于样本量为10的上述调查结果经计算,细心护理型占50%,粗放型30%,异常数据20%。
变量性问题平均值:

对于各个角色均值数据如下:

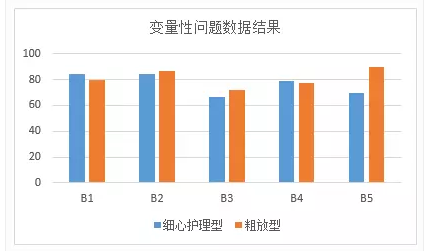
从上述数据结论可知,对呀B1-B4问题,两个用户角色观点相差不大。但是对于B5(产品交互)问题粗放型用户比细心护理型用户更为重视。
经过对建议性问题分析结果可以得到如下图表:
由此可得出结论,细心护理型用户对email的要去较为强烈;粗放型的用户倾向与写信的方式。对于添加的服务项,这两种角色均有需求。

综上所述,我们只是举了一个非常非常2b又简单的例子来说明构建用户模型的方法,实验的样本量也很小。这个简单的例子可以说明基本方法,要真正应用到自己的case中,还需要认真研究分析。
多元回归方法分析用户模型
对于数学好的童鞋,可以给出一种多元回归统计的方法来分析我们得到的数据。这里写的并不详细,也没听提供假设检验,望高手多多指点交流。我们仅用多元回归方法来分析变量性问题的结果。
我们的例子提出了5个变量性问题,所以要回归的线性方程具有5个变量,形式如下:
Y=b0+b1x1+b2x2+b3x3+b4x4+b5x5
我们的目的就是要对b0、b1、b2…b5计算出估计量。
写成矩阵的形式为Y=BX
其中Y为综合满意度数据

B是我们要估计的矩阵
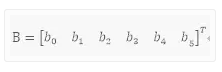
使用MATLAB中的regress(y,x)可以对B进行多元回归,结果如下:
(这里没有进行假设检验等,大家可以自行完善)
>> y=load('C:\Users\ydbj0017\Desktop\y.txt')
y =
90
85
77
81
70
78
89
91
90
80
>> x=load('C:\Users\ydbj0017\Desktop\x.txt')
x =
1 80 95 79 78 67
1 87 66 60 89 78
1 97 77 87 69 90
1 88 98 65 75 68
1 78 83 63 73 76
1 73 75 88 80 95
1 78 98 63 66 97
1 77 74 87 66 69
1 90 88 67 87 78
1 88 78 67 79 60
>> regress(y,x)
ans = %这个就是估计矩阵B
51.4213 %b0
-0.0868 %b1
0.2210 %b2
0.1407 %b3
0.2041 %b4
-0.0671 %b5
b0为常数,对变量没有影响,剩余对应相应的变量问题。由此可见B2问题是全部用户对整体评价中权重最大的因素。



